Частота колебаний -формулы определения, от чего зависит

Формулы периода и частоты колебаний

ОПРЕДЕЛЕНИЕ

Период колебаний – это время, за которое тело совершает одно полное колебание.

Единица измерения периода в системе СИ – секунда.

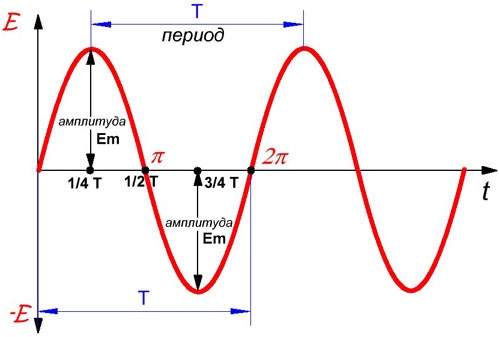
На графике колебаний период определяется как промежуток времени. через который система возвращается в то же состояние, в котором она находилась в начальный момент времени, который выбирается произвольно (рис.1).

Рис.1. Определение по графику периода колебаний.

ОПРЕДЕЛЕНИЕ

Частота колебаний – это число колебаний, совершаемых телом в единицу времени:

Единица измерения частоты в системе СИ – 1 Герц (Гц).

ОПРЕДЕЛЕНИЕ

Циклическая частота – это число колебаний, совершаемых телом за секунд:

Единица измерения циклической частоты в системе СИ — рад/с.

Частота и циклическая частота связаны между собой формулой:

Математический маятник

Эта модель рассматривает движение груза, подвешенного на нитке. Описывается система, в которой масса нитки намного меньше массы груза, а ее длина намного больше его размеров.

Также нить должна быть невесомой и нерастяжимой.

Груз в этом случае считается материальной точкой.

При выполнении этих условий частота колебаний маятника и период не будут зависеть от массы груза. Движение математического маятника рассматривается при небольшом угле отклонения (α). Последний измеряется в радианах, поэтому приблизительно соответствует по значению его синусу и тангенсу. Этот же угол пропорционален отношению смещения на длину нити:

α=x/l.

На маятник действует синусовая составляющая силы тяжести и тангенсовая сила натяжения нити. Согласно второму закону Ньютона: ma=-mgsin (α). Откуда можно получить a=-gx/l

Вторая производная уравнения движения дает a=-(ω)^2x

Таким образом: -gx/l=-(ω)^2x -> ω ^2=g/l.

Период: T=2π /ω T=2π*sqrt (g/l)

Это формула Галилея, которая описывает движение математического маятника.

Формула частоты колебаний для математического маятника: v=sqrt (l/g)/2π.

Видео

Что такое частота

Обозначают ее с помощью греческой буквы «ню» \( \large \nu \).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

\( \large \nu \left( \frac{1}{c} \right) \).

Иногда в учебниках встречается такая запись \( \large \displaystyle \nu \left( c^{-1} \right) \), потому, что по свойствам степени \( \large  \displaystyle \frac{1}{c} = c^{-1} \).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

\[ \large \displaystyle \boxed{ \frac{ 1 \text{колебание}}{1 \text{секунда}} = 1 \text{Гц} }\]

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

\[ \large \boxed{ \nu = \frac{1}{T} }\]

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду

Частота колебаний

Частота служит одним из основных параметров, характеризующих колебания.

Определение

Частота — это физическая величина обратная периоду колебаний (T). Частота — это число полных колебаний, которые совершаются за единицу времени. \[\nu =\frac{1}{T}\left(1\right).\]

В Международной системе единиц (СИ) частота измеряется в герцах или обратных секундах:

Герц — единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, о близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:

Другой характеристикой колебаний является циклическая частота, которая равна:

Циклическая частота измеряется в радианах, деленных на секунду:

Частота колебаний тела, массой$\ m,$ подвешенного на пружине с жесткостью $k$ равна:

Выражение (4) выполняется для упругих, малых колебаний. Масса пружины должна быть мала в сравнении с массой тела.

Частота колебаний математического маятника, длина нити которого $l$:

где $g$ — ускорение свободного падения.

Частота колебаний физического маятника:

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее результаты дают эти формулы.

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_{0} \).

\(\large \varphi_{0} \left(\text{рад} \right) \) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний

Рассмотрим теперь, как величина \(\large \varphi_{0} \) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_{0} \) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_{0} \) будет отличаться от нулевого значения.

Определим угол \(\large \varphi_{0} \) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_{0} \) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_{0} \).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

• Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал \(\large \Delta t\) равен 1 сек.
• Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

\[\large T = 5 – 1 = 4 \left( \text{сек} \right)\]

Из графика следует, что период T = 4 сек.

• Рассчитаем теперь, какую долю периода составляет интервал времени \(\large \Delta t\). Для этого составим такую дробь \(\large \displaystyle \frac{\Delta t }{T} \):

\[\large \frac{\Delta t }{T} = \frac{1}{4} \]

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

• Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол \(\large 2\pi \). Найдем теперь, как связана найденная доля периода с углом \(\large 2\pi \) полного цикла.

Для этого используем формулу:

\[\large \boxed{ \frac{\Delta t }{T} \cdot 2\pi = \varphi_{0} }\]

\(\large \displaystyle \frac{1}{4} \cdot 2\pi = \frac{\pi }{2} =\varphi_{0} \)

Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac{\pi }{2} \) – это начальная фаза для красной кривой на рисунке.

• В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

\[\large \varphi_{0} = — \frac{\pi }{2} \]

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac{\pi }{2} \) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая \(\large \varphi_{0} = 0 \).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину \(\large \varphi_{0} \) записываем со знаком «-».

Примечания:

1. Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
2. На графике колебаний начальная фаза \( \varphi_{0}\) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Явление резонанса

Это понятие имеет особое значение для описания колебаний. Если имеется некое воздействие, частота которого приближается к собственной частоте системы, то последняя реагирует резким увеличением амплитуды.

Явление резонанса можно представить себе на примере того же математического маятника. Для этого необходимо маятник привязать к веревке, к которой привязать еще один такой же, но с более длинной нитью. При этом длина нитки второго маятника может регулироваться. Если привести в движение оба маятника, а длину второй нитки постепенно изменять, то можно будет заметить, что амплитуда увеличивается по мере приближения размеров обеих ниток.

В этом случае первый маятник будет приемником колебаний, а второй — передатчиком. Причиной увеличения амплитуды является колебание подвески с такой же частотой.

Примеры решения задач

ПРИМЕР 1

Задание Определить частоту колебаний железнодорожных вагонов, если период их вертикального колебания равен 0,5 с. Решение Частота колебаний – это величина, обратная периоду: Гц Ответ Частота колебаний вагонов 2 Гц.

ПРИМЕР 2

Задание Маятник совершает 9 колебаний за 18 с. Определить период и частоту колебаний. Записать уравнение гармонических колебаний и построить график колебаний маятника, если амплитуда равна 10 см. Решение Частота колебаний определяется формулой: Гц Циклическая частота: Период колебаний: В общем виде уравнение гармонических колебаний: В данном случае: График колебаний: Ответ Частота колебаний 0,5 Гц; период колебаний 2 с; уравнение колебаний

ПРИМЕР 3

Задание Период колебаний крыльев шмеля 5 мс, а частота колебаний крыльев комара 600 Гц. Определить, какое насекомое и на сколько больше сделает взмахов крыльями при полете за 1 минуту. Решение Определим частоту колебаний крыльев шмеля: С другой стороны, частота: Приравняв правые части равенств, найдем число взмахов крыльями, которое сделает шмель за время : Число взмахов крыльями, которое сделает комар за время , найдем непосредственно из формулы: Переведем единицы в систему СИ: мс мин . Вычислим: Ответ Комар сделает на 24000 взмахов крыльями больше, чем шмель.

Теги