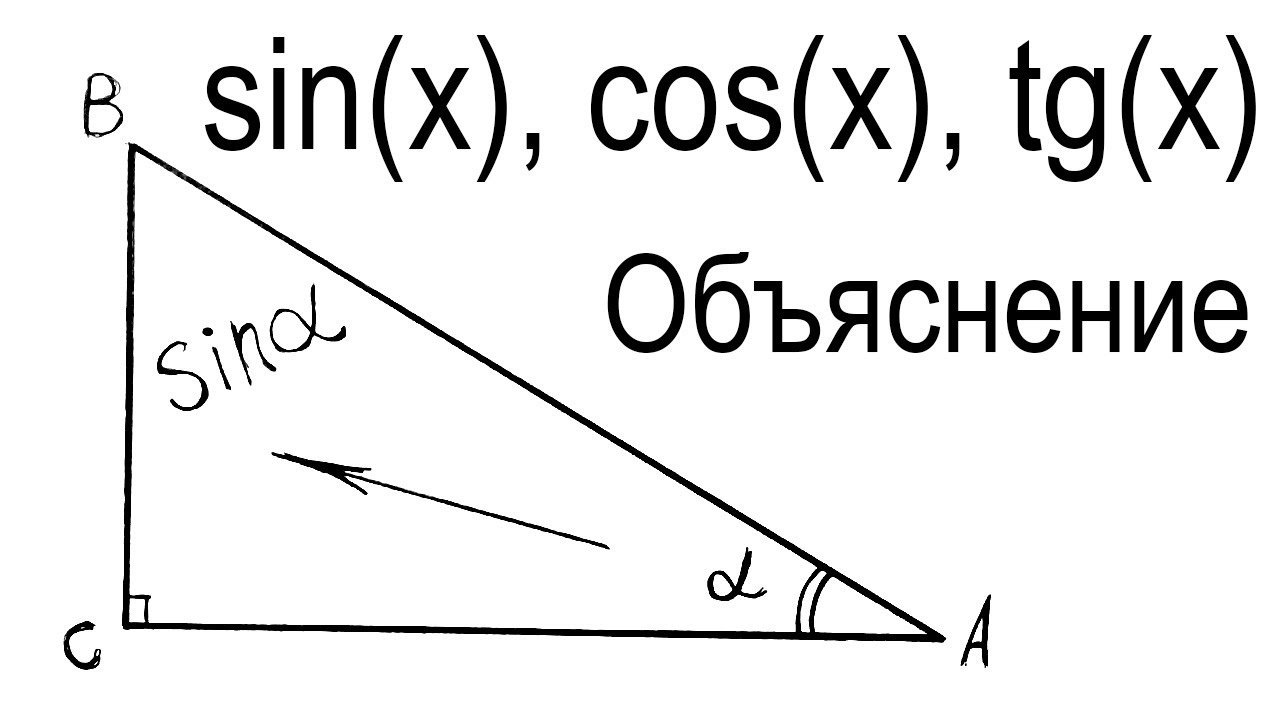Свойства ⭐ синусов и косинусов с подробными пояснениями

Связь между sin и cos одного угла

Вы уже наверняка знаете, что тождественный — это равный. 

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция. 

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

sin2α + cos2α = 1 Читайте также: Значение слова РАЗНОСТЬ. Что такое РАЗНОСТЬ?

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg²α + 1 = 1/cos²α и равенство 1 + сtg²α + 1 = 1/sin²α выводят из основного тождества, разделив обе части на sin²α и cos²α.

В результате деления получаем:

Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая. 

sin²α + cos²α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.

Чтобы доказать тождество, обратимся к теме единичной окружности. 

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

Докажем тождество sin²α + cos²α = 1

1. Итак, нам известны координаты точки A (1; 0). Произвольный угол α, тогда cos α = x0 = ОB.
2. Если развернуть точку A на угол α, то точка A становится на место точки A₁.
3. По определениям:
   • Синус угла (sin α) — это отношение противолежащего катета к гипотенузе. 
   • Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
   Это значит, что точка A₁ получает координаты cos α, sin α.
4. Опускаем перпендикулярную прямую A₁B на x0 из точки A₁. Образовался прямоугольный треугольник OA₁B. |A₁B| = |у| |OB| = |x|.
5. Гипотенуза OA₁ имеет значение, равное радиусу единичной окружности. |OA₁| = 1.
6. Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой: |A₁B|² + |OB|² = |OA₁|².
7. Записываем в виде: |y|² + |x|² = 1². Это значит, что y² + x² = 1. sin угла α = y cos угла α = x
8. Вставляем данные угла вместо координат точек: OB = cos α A₁B = sin α A₁O = 1
9. Получаем основное тригонометрическое тождество: sin²α + cos²α = 1. Что и требовалось доказать. 

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

• sin α = ±
• cos α = ±

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

Видео

Cинус, косинус, тангенс, котангенс угла в прямоугольном треугольнике

Итак, с понятием угла разобрались. А что же всё-таки такое синус, косинус, тангенс, котангенс угла?

Давай разбираться. Для этого нам поможет прямоугольный треугольник.

Как называются стороны прямоугольного треугольника?

Всё верно, гипотенуза и катеты.

Гипотенуза — это сторона, которая лежит напротив прямого угла (в нашем примере это сторона \( AC\))

Катеты – это две оставшиеся стороны \( AB\) и \( BC\) (те, что прилегают к прямому углу).

Причём, если рассматривать катеты относительно угла \( \angle BAC\), то катет \( AB\) – это прилежащий катет, а катет \( BC\) — противолежащий.

Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?

Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе.

В нашем треугольнике \( \sin \beta =\frac{BC}{AC}\).

Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.

В нашем треугольнике \( \cos \beta =\frac{AB}{AC}\).

Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).

В нашем треугольнике \( tg\beta =\frac{BC}{AB}\).

Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).

В нашем треугольнике \( ctg\beta =\frac{AB}{BC}\).

Эти определения необходимо запомнить!

Чтобы было проще запомнить какой катет на что делить, необходимо чётко осознать, что в тангенсе и котангенсе сидят только катеты, а гипотенуза появляется только в синусе и косинусе.

А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:

Косинус→касаться→прикоснуться→прилежащий;

Котангенс→касаться→прикоснуться→прилежащий.

В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле).

Не веришь?

Тогда убедись, посмотрев на рисунок:

Рассмотрим, к примеру, косинус угла \( \beta \).

По определению, из треугольника \( ABC\): \( \cos \beta =\frac{AB}{AC}=\frac{4}{6}=\frac{2}{3}\).

Но ведь мы можем вычислить косинус угла \( \beta \) и из треугольника \( AHI\): \( \cos \beta =\frac{AH}{AI}=\frac{6}{9}=\frac{2}{3}\).

Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.

Если разобрался в определениях, то вперёд закреплять их!

Для треугольника \( ABC\), изображённого ниже на рисунке, найдём \( \sin \ \alpha ,\ \cos \ \alpha ,\ tg\ \alpha ,\ ctg\ \alpha \).

\( \begin{array}{l}\sin \ \alpha =\frac{4}{5}=0,8\\\cos \ \alpha =\frac{3}{5}=0,6\\tg\ \alpha =\frac{4}{3}\\ctg\ \alpha =\frac{3}{4}=0,75\end{array}\)Ну что, уловил?

Тогда пробуй сам: посчитай то же самое для угла \( \beta \).

Ответы: \( \sin \ \beta =0,6;\ \cos \ \beta =0,8;\ tg\ \beta =0,75;\ ctg\ \beta =\frac{4}{3}\).

Тангенс и косинус, котангенс и синус

Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла  — с синусом.

Эта связь становится очевидна, если взглянуть на тождества:  

• tg²α + 1 =

Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.

• 1 + ctg²α =

Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.

Вывести оба этих тождества можно из основного тригонометрического тождества: sin²α + cos²α = 1.  

1. Для этого нужно поделить обе части тождества на cos²α, где косинус не равен нулю.
2. В результате деления получаем формулу tg²α + 1 =
3. Если обе части основного тригонометрического  тождества sin²α + cos²α = 1 разделить на  sin²α, где синус не равен нулю, то получим тождество: 1 + ctg²α = . 
4. Отсюда можно сделать вывод, что тригонометрическое тождество tg²α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
5. А тригонометрическое тождество 1 + ctg²α = применимо для любого угла, не равного π * z, где z — это любое целое число. 

Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами. 

Основные тригонометрические тождества

1	sin2α + cos2α = 1
2
3
4	tgα * ctgα = 1
5	tg2α + 1 =
6	1 + ctg2α =

Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.

Табличные значения синуса и косинуса

Нулевой угол \( \LARGE 0^{\circ } \)

Абсцисса точки равна 1, ордината точки равна . Следовательно,

cos 0 = 1   sin 0 = 0

Рис 4. Нулевой угол

Угол \( \LARGE \frac{\pi}{6} = 30^{\circ } \)

Мы видим прямоугольный треугольник с единичной гипотенузой и острым углом 30°. Как известно, катет, лежащий напротив угла 30°, равен половине гипотенузы¹; иными словами, вертикальный катет равен 1/2 и, стало быть,

\[ \sin \frac{\pi}{6} =\frac{1}{2} \]

Горизонтальный катет находим по теореме Пифагора (или, что то же самое, находим косинус по основному тригонометрическому тождеству):

\[ \cos \frac{\pi}{6} = \sqrt{1 — \left(\frac{1}{2} \right)^{2} } =\frac{\sqrt{3} }{2} \]

¹ Почему так получается? Разрежьте равносторонний треугольник со стороной 2 вдоль его высоты! Он распадётся на два прямоугольных треугольника с гипотенузой 2, острым углом 30° и меньшим катетом 1.

Рис 5. Угол π / 6

Угол \( \LARGE \frac{\pi}{4} = 45^{\circ } \)

В данном случае прямоугольный треугольник является равнобедренным; синус и косинус угла 45° равны друг другу. Обозначим их пока через x. Имеем:

\[ x^{2} + x^{2} = 1 \]

откуда \( x=\frac{\sqrt{2} }{2} \). Следовательно,

\[ \cos \frac{\pi}{4} = \sin \frac{\pi}{4} =\frac{\sqrt{2} }{2} \]

Рис 5. Угол π / 4

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от $—\infty$ до $+\infty$. 

Свойства синуса и косинуса

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).

y = sin x	y = cos x
Область определения и непрерывность	– ∞ < x < + ∞	– ∞ < x < + ∞
Область значений	–1 ≤ y ≤ 1	–1 ≤ y ≤ 1
Возрастание
Убывание
Максимумы, y = 1
Минимумы, y = –1
Нули, y =
Точки пересечения с осью ординат, x =	y =	y = 1

Тригонометрические функции углового и числового аргумента

Каждому значению угла $\alpha$ соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам $\alpha$, отличным от α = 90 ° + 180 ° · k ,   k ∈ Z   ( α = π 2 + π · k ,   k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех $\alpha$, кроме α = 180 ° · k ,   k ∈ Z   ( α = π · k ,   k ∈ Z ). 

Можно сказать, что $\sin \alpha , \cos \alpha , tg \alpha , ctg \alpha$ — это функции угла альфа, или функции углового аргумента. 

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k ,   k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k ,   k ∈ Z.

Синус, косинус, тангенс и котангенс — основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело. 

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.

Арксинус, arcsin

\( y = \arcsin x \) \( \left\{ -1 \leqslant x \leqslant 1; \; — \dfrac{\pi}2 \leqslant y \leqslant \dfrac{\pi}2 \right\} \)\( \sin( \arcsin x ) = x \) \( \{ -1 \leqslant x \leqslant 1 \} \)\( \arcsin( \sin x ) = x \) \( \left\{ — \dfrac{\pi}2 \leqslant x \leqslant \dfrac{\pi}2 \right\} \)

Теги