Содержание материала
Что такое пропорция?
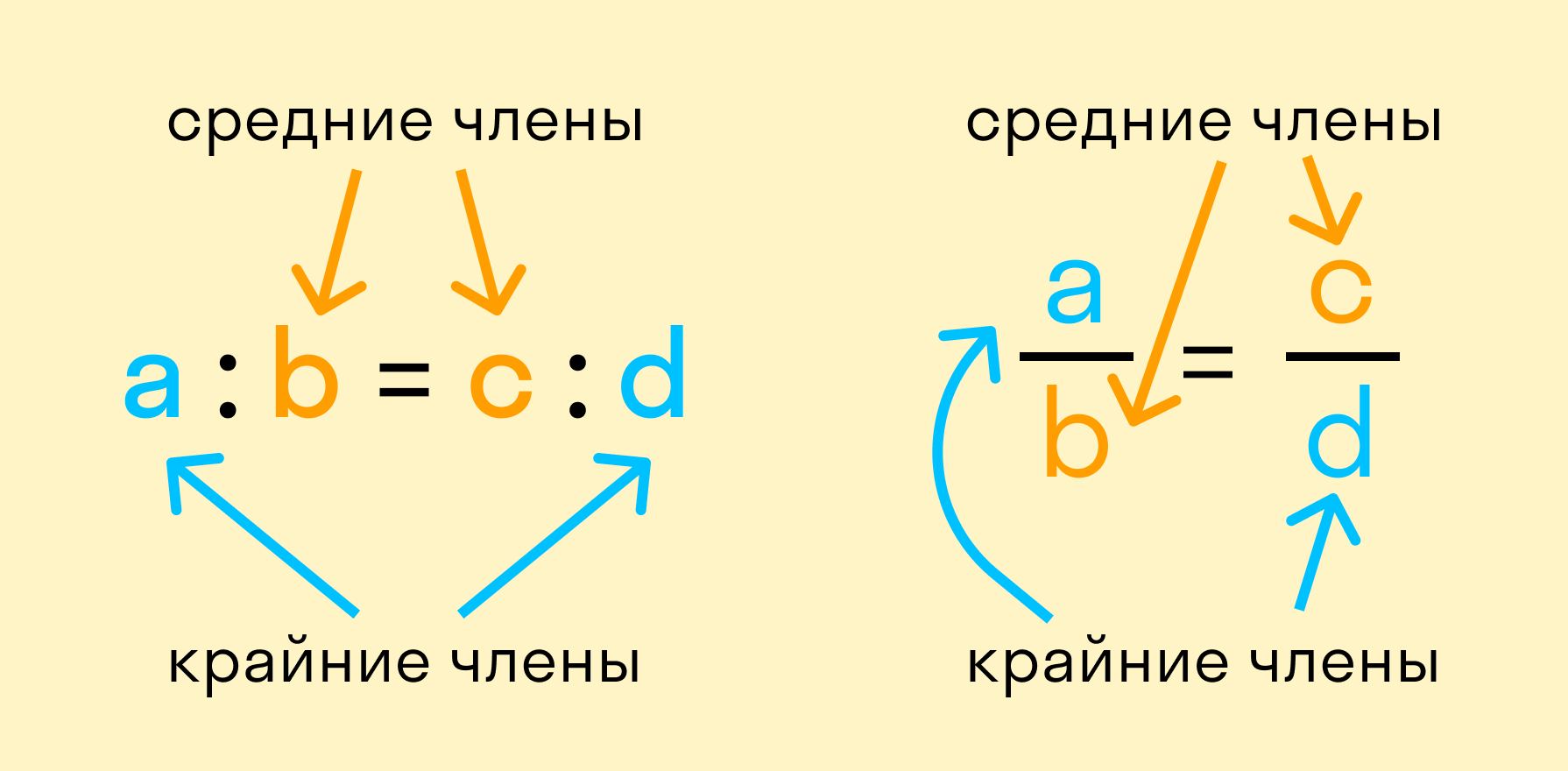
Определение Пропорция — это верное равенство двух отношений. 
Где a ? 0, b ? 0, c ? 0, d ? 0. a и d — называют крайними членами пропорции; b и c — называют средними членами пропорции.
| 3 | = | 18 | или 3 : 5 = 18 : 30; |
| 5 | 30 |
| 7 | = | 21 | или 7 : 3 = 21 : 9; |
| 3 | 9 |
| 12 | = | 48 | или 12 : 15 = 48 : 60. |
| 15 | 60 |
Основное свойство пропорции
Свойство
Произведение крайних членов пропорции равно произведению ее средних членов. Пример | 12 | = | 24 | , значит 12 • 8 = 4 • 24; |
| 4 | 8 |
| 11 | = | 33 | , значит 11 • 21 = 7 • 33; |
| 7 | 21 |
| 23 | = | 69 | , значит 23 • 42 = 14 • 69. |
| 14 | 42 |
Производные пропорции
Правило
Пример | 4 | = | 8 | или | 7 | = | 14 | или | 8 | = | 17 | или | 4 | = | 7 | ; |
| 7 | 14 | 4 | 8 | 4 | 7 | 8 | 14 |
| 5 | = | 10 | или | 6 | = | 12 | или | 10 | = | 12 | или | 5 | = | 6 | ; |
| 6 | 12 | 5 | 10 | 5 | 6 | 10 | 12 |
| 9 | = | 18 | или | 3 | = | 6 | или | 6 | = | 18 | или | 9 | = | 3 | . |
| 3 | 6 | 9 | 18 | 3 | 9 | 18 | 6 |
| 15 | = | x | , значит x = | 15 • 14 | = 15 • 2 = 30; |
| 7 | 14 | 7 |
| 21 | = | x | , значит x = | 21 • 9 | = 21 • 3 = 63; |
| 3 | 9 | 3 |
| 33 | = | 99 | , значит x = | 4 • 99 | = 4 • 3 = 12. |
| 4 | x | 33 |
Основное свойство пропорции
Запомните основное свойство пропорции:
| Произведение крайних членов пропорции равно произведению средних членов этой пропорции. |
В виде формулы свойство выглядит так:
a : b = c : d a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
- Чтобы проверить, верно ли составлена пропорция, перемножаем ее крайние члены: 6 * 4 = 24.
- Далее перемножаем средние члены пропорции: 2 * 12 = 24
- Произведение крайних членов пропорции равно 24, произведение средних членов пропорции также равно 24.
- 6 * 4 = 2 * 12 24 = 24
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
- Перемножаем крайние члены пропорции: 10 * 4 = 40.
- Перемножаем средние члены: 16 * 2 = 32.
- Произведение крайних членов пропорции равно 40. Произведение средних членов пропорции равно 32.
- 10 * 4 ≠ 16 * 2 40 ≠ 32
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео
Составление и решение пропорций
Запишите пропорцию: 6 так относится к 18, как 9 относится к 27. Решение. Слово «относится» заменяем на знак деления. Получаем два отношения: 6:18 и 9:27. Если эти два отношения равны, то получаем верную пропорцию. 6:18=9:27;13=13, получили верную пропорцию.
Запишите пропорцию и проверьте ее: отношение 2 к 14 равно отношению 3 к 115. Решение. Записываем отношения: 214и3115. Составляем пропорцию: 214=3115. Проверяем, верна ли пропорция. Для этого воспользуемся основным свойством пропорции: произведение крайних членов = произведению средних членов. 2*115≠14*3;215≠34. Условие равенства произведений не выполнилось, значит, пропорция не верна.
Определите, верна ли пропорция: 1,4,7=3,41,7. Решение. Чтобы проверить, верна ли пропорция, воспользуемся основным свойством пропорции. Запишем произведения крайних и средних членов пропорции: 1,4*1,7=2,38;,7*3,4=2,38. Значит, произведение крайних членов равно произведению средних членов. 1,4*1,7=,7*3,4;2,38=2,38. Вывод: пропорция верна.